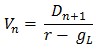Модель дисконтирования дивидендов (DDM)

08.08.201808.08.2018 by Ваш Казначей

Что такое модель дисконтирования дивидендов (DDM) для оценки справедливой стоимости акций? Как и когда используются различные варианты модели DDM: для фиксированного размера выплат, модель Гордона и многоэтапные модели?

Что такое Dividend Discount Model?

Существует несколько моделей оценки справедливой стоимости акций компании, но нет ни одной универсальной. Все эти модели имеют свои преимущества, недостатки и ограничения в использовании. Пожалуй, самой простой и распространенной из них является модель дисконтирования дивидендов – DDM (англ. Dividend Discount Model).

Это модель также строится на основании DCF анализа (англ. Discount Cash Flow), как и модель оценки стоимости бизнеса с помощью свободного денежного потока FCFF или FCFE.

Суть данной модели в том, что в качестве ожидаемых денежных потоков по оцениваемому активу (привилегированной или обыкновенной акции компании) используется прогнозируемый размер дивидендов корпорации-эмитента, сумма которых дисконтируется (приводится к текущей стоимости с помощью коэффициента дисконтирования).

Исходя из этого определения, можно сразу определить основное ограничение использования модели: она не подходит для оценки стоимости акций компаний, не выплачивающих дивиденды (поскольку довольно трудно строить прогнозы относительно размера дивидендных выплат для эмитентов, которые не имеют дивидендной истории).

Тем не менее, благодаря своей простоте и прозрачности данный метод оценки весьма широко распространен в финансовом мире.

Модель DDM включает в себя 4 основных показателя:

Текущая цена акции (P),
Размер дивиденда (Div),
Темп роста (g),
Ставка дисконтирования (r).

Отсюда вытекает второй недостаток: результат, получаемый посредством модели DDM очень чувствителен к изменению темпа роста (g) и ставки дисконтирования (r), а процесс определения этих показателей весьма субъективен.

Кроме того, модель DDM не подойдет для оценки стоимости акций компаний, чья динамика денежных потоков характеризуется ярко выраженной цикличностью (например, компаний, производящих или продающих товары/услуги длительного спроса: автомобили, технику, мебель, развлечения и т.п.) или только еще находящихся на стадии своего развития.

Таким образом, DDM – это модель для оценки:

стабильно растущих,
нецикличных компаний, чьи объемы продаж стабильны в любой фазе развития экономики (например, производителя продуктов питания),
имеющих богатую дивидендную историю.

В общем виде формула DDM для условно бесконечного потока дивидендов выглядит следующим образом:

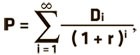
где:

P – текущая справедливая цена акции,

r — ставка дисконтирования (требуемая доходность),

D_i— дивиденды i-го года.

Для стабильного (фиксированного) размера дивидендных выплат и неизменной ставки дисконта формула имеет более простой вид:

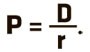
Частный случай модели DDM, предполагающий стабильный темп прироста дивидендов (по ставке g) и постоянную ставку дисконта r, называется моделью Гордона (или моделью постоянного роста).

[irp]

Модель Гордона

Как уже было сказано выше модель Гордона предполагает, что дивиденды растут бесконечно по фиксированной ставке g. К данной модели применима следующая общая формула:

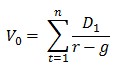
где:

D₁ – дивиденды 1-го года,

r — ставка дисконтирования (требуемая доходность),

g – темп прироста (процентная ставка, выраженная десятичной дробью).

Прогнозирование размера дивиденда в следующем периоде (D1) складывается из значения чистой прибыли в последнем отчетном периоде, темпа роста и процентной доли доходов, выплачиваемых в виде дивидендов.

D₁ = прибыль за последний период * коэффициент выплаты дивидендов * (1+g)

Аналитики используют следующую формулу для расчета ставки g:

g = доля нераспределяемой прибыли x ROE

Доля нераспределяемой прибыли рассчитывается как (1 – % отношение суммы дивидендов к совокупной прибыли).

ROE (Return On Equity) – это коэффициент отдачи собственного капитала, который показывает, сколько прибыли приходится на одну денежную единицу, вложенную в собственный капитал. Рассчитывается как отношение чистой прибыли к среднему размеру собственного капитала.

Кроме модели Гордона, DDM имеет и более сложные варианты в виде двухэтапных и трехэтапных моделей роста дивидендов. Безусловно эти модели более приближены к реальным бизнес-циклам и динамике дивидендной политики. Суть этих моделей состоит в том, что для каждого этапа (например, высокого, переходного и стабильного) применим разный темп роста дивидендов и расчет стоимости актива на каждом этапе производится отдельно.

[irp]

Двухэтапная модель дисконтирования дивидендов

Двухэтапная модель DDM предполагает наличие первого краткосрочного этапа, в рамках темп роста дивидендов довольно высок, и второго долгосрочного этапа, на котором темп прироста дивидендов резко снижается и остается постоянным (в трехэтапном модели между этими двумя этапами будет переходный тап, на протяжении которого темп роста дивидендов снижается постепенно).

Справедливая стоимость акций компании в таком случае оценивается следующим образом:

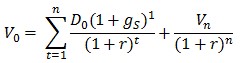
D_n+1 = D₀(1 + g_S)ⁿ * (1 + g_L)

где:

V_o_,_n – справедливая стоимость акции,

D _o_,_n – дивиденды,

n – количество периодов с высоким темпом роста,

g_S – краткосрочный темп роста,

g_L – долгосрочный темп роста.

Пример:

Оценим справедливую стоимость акций со следующими вводными данными:

последний размер дивидендных выплат на 1 обыкновенную акцию составил 2.5 рубля.
В ближайшие 2 года темп прироста дивидендов составит 20%.
Начиная с третьего года прогнозного периода тем прироста дивидендов снизится до 3%.
Требуемая доходность по акциям – 14%.

Расчет будем производить по модели DDM в несколько этапов:

1/ Рассчитаем текущую (приведенную) стоимость денежных потоков для первого этапа (Год 1 и Год 2):

2,5* 1,2 /1,14+2,5*(1,20)² /(1,14)² = 5,40